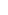[Когда доказано, что ord(X,s)=(i∈Z)Σ(−1)^(i+1)·dimQ·Ki'(X)(n), существует Cq(D,k)={ (f(x1),···, f(xn))∈Fnq|f(x)∈Fq[x], degf(x)≤k−1…]
Кабинет в здании математического факультета Университета Цзинь Лин.
Шольце, а также недавно присоединившиеся к исследовательской группе участники Теории Великого Объединения стояли перед доской, уставившись на густо исписанные уравнениями листы. Через пять минут Лу Чжоу потёр подбородок и дал оценку.
«Это очень интересная идея».
Перельман кивнул, соглашаясь с Лу Чжоу, и сказал: «Верно, это очень новая идея».
Фальтингс ничего не сказал, но по выражению его лица было ясно, что он согласен.
Шольце улыбнулся и сказал: «Вот что я обнаружил, когда изучал полное метрическое пространство, и это открытие вдохновило меня на создание теории Великого объединения. Я потратил год на её совершенствование. Если мы сможем найти точное выражение для Cq(D, K) и подставить его в уравнение 4, то сможем связать H(v) с неприводимыми мотивами».
Лу Чжоу кивнул: «Да, тогда мы можем косвенно изучить разложение теории мотивов на прямую сумму с помощью функции H(v)».
Профессор Фальтингс, который никогда не любил хвалить других, не мог не восхищаться умом Шольце. Его полная теория метрического пространства сыграла неожиданную роль в теории мотивов. Что было ещё более удивительным, так это то, что по сравнению с такими учёными, как Перельман, которые предпочитали заниматься наукой за закрытыми дверями, Шольце был гораздо лучшим оратором. В целом, убедить других учёных заняться какой-либо областью исследований было почти так же сложно, как и провести само исследование. В конце концов, независимо от того, было ли это сложное или простое математическое утверждение, потребовалось бы много времени, чтобы полностью понять саму проблему. Люди изучали бы проблему только в том случае, если бы считали её достаточно важной.
Шольце улыбнулся в знак одобрения Лу Чжоу и сказал: «Кстати, я ещё не дал этому методу название».
Лу Чжоу на секунду задумался и сказал: «А как насчёт теории применения двойственности Пуанкаре? Я заметил, что основная часть теории — это обобщение теории двойственности Пуанкаре на многомерные числа когомологий».
— Это слишком сложно запомнить, в наши дни популярны короткие названия, например… — Шольце на секунду задумался и сказал: — Как насчёт теории складок? С абстрактной точки зрения мы складываем набор алгебраических выражений.
Когда Лу Чжоу услышал это имя, он был озадачен. Он подумал, что это имя вообще не имеет никакого отношения к теореме. Чэнь Ян и Перельман не особо заботились о таких мелочах. Профессор Фальтингс, напротив, явно был согласен с Лу Чжоу. Он покачал головой и сказал: «Вы, миллениалы, любите придумывать причудливые имена. Я думаю, что имя профессора Лу довольно хорошее».
Лу Чжоу: «…»
Несмотря на то, что он был рад, что профессор Фальтингс согласился с ним, он чувствовал, что Фальтингс называет его стариком.
Пока в кабинете обсуждали важные вопросы, все остальные молчали. Хань Мэнци уставилась на уравнения на доске и нахмурилась. Ей казалось, что она почти понимает, что происходит. Хэ Чанвэнь тоже нахмурился с серьёзным выражением лица.
Читайте ранобэ Передовая Технологическая Система Учёного на Ranobelib.ru
Что касается Ли Мо…
Он был ошеломлён.
Долгое время он считал, что находится очень близко к границам математики, особенно когда Лу Чжоу согласился принять его в проект «Теория великого объединения». Он был уверен, что сможет стать выдающимся учёным. Но это был огромный удар по его гордости. Забудьте о том, чтобы разговаривать с этими мастерами, он даже не мог понять, о чём говорят эти великие умы. Неудивительно, что эти ребята — лауреаты Филдсовской премии… Как страшно!
Ли Чжун посмотрел на доску и сглотнул. Он сказал: «Братан… Как они получили значение k в уравнении 8? Я не понимаю».
«Просто будь внимателен», — сказал Хэ Чанвэнь, уставившись на доску. Ли Мо подумал, что прерывает мыслительный процесс Хэ Чанвэня, и закрыл рот. Через некоторое время Хэ Чанвэнь нахмурился и опустил голову. Он тихо спросил Хань Мэнци: «Как они вывели уравнения 1 и 2? Вы видели их раньше?»
Хань Мэнци сказал: «… Я думаю, что это следствие гипотезы Вейля».
Ли Мо: «…»
…
Лу Чжоу предложил схему для решения всего предложения. В то время как метод, предложенный Шольце, давал ответ на конкретную проблему в рамках этой схемы.
На самом деле метод предполагал, что знаменитая гипотеза Бейлинсона-Блоха-Като в алгебраической геометрии верна. Доказать эту гипотезу было непросто, и Шольце потратил последний год на поиски доказательства. Если бы не было способа доказать, что гипотеза Бейлинсона-Блоха-Като верна, то его метод «сгибания» был бы бесполезен. Однако, поскольку Лу Чжоу был здесь, Шольце не беспокоился. Эта задача определённо была проще, чем гипотеза Римана. Особенно для Лу Чжоу. Никто не умел находить доказательства лучше Лу Чжоу. Обсуждение продолжалось.
Лу Чжоу предлагал метод, позволяющий связать K-группу высокого порядка эллиптической кривой E с аналитическим инвариантом для решения гипотезы Бейлинсона — Блоха — Като. Внезапно телефон в его кармане завибрировал. Хотя он и не хотел отвечать на звонок, это могло быть что-то важное. Когда Лу Чжоу увидел, что звонит Чэнь Юйшань, он подумал, что в Star Sky Technology что-то случилось. Он указал на свой телефон и сказал.
«Прошу прощение это по работе».
Шольце улыбнулся и сказал: «Конечно, мне всё равно нужно время, чтобы обдумать ваш метод».
Лу Чжоу кивнул и пошёл по коридору. Он взял трубку и сразу же услышал голос Чэнь Юйшаня. «Проверь Weibo!»