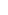На самом деле, даже Лу Чжоу не был уверен, человек он или нет. Судя по результатам его медицинского обследования, высокотехнологичная система не повлияла на его ДНК. Однако его когнитивные способности значительно превосходили уровень обычных людей. Если он правильно помнит, когда он впервые приехал в Принстон около шести лет назад, профессор Делинь пригласил его принять участие в исследовании стандартных гипотез Гротендика. С тех пор прошло шесть лет. До сих пор не было достигнуто никакого значительного прогресса в решении этой проблемы. Теперь решить её было так же просто, как прогуляться. Несмотря на то, что основной причиной решения этой проблемы была теоретическая основа, которую обеспечивала теория Великого объединения, возможность сделать выводы с помощью теории Великого объединения за полчаса всё равно была невероятно впечатляющим достижением. Даже Лу Чжоу был впечатлен самим собой. Лу Чжоу сделал глубокий вдох и попытался успокоиться. Он уставился на надпись «Гипотеза Лефшеца верна!» и заговорил после минутного молчания.
«Всем известно, что стандартные гипотезы Гротендика можно разделить на две части. Первая часть — это обобщение теоремы Харда Лефшеца, сделанное профессором Гротендиком, то, что мы знаем как стандартная гипотеза Лефшеца. Вторая часть — это стандартная гипотеза Ходжа».
Лу Чжоу нахмурился и надолго задумался.
В зале стояла тишина.
Все ждали, когда он продолжит.
Под взглядами бесчисленных участников Лу Чжоу внезапно расслабился и заговорил непринуждённым тоном.
«Неважно. Хотя я просто демонстрировал применение теории Великого объединения в алгебраической геометрии… Я уже так много написал. С таким же успехом можно закончить».
Лу Чжоу не заметил удивлённых взглядов, брошенных ему вслед, и не обратил внимания на недоверчивые возгласы. Лу Чжоу подошёл к пустой доске со спокойным и расслабленным выражением лица. Он остановился на мгновение. Стандартные гипотезы Гротендика были одними из самых глубоких утверждений в алгебраической геометрии. Красота гипотез заключалась не только в их сложности, но и в выводах. Если бы стандартные гипотезы Гротендика оказались верными, их можно было бы напрямую использовать для доказательства гипотезы Вейля. Также можно было бы сделать вывод, что функция Фробениуса в группе когомологий гладких алгебраических многообразий является полупростой и что алгебраический цикл, гомологическая эквивалентность и числовая эквивалентность связаны замкнутой цепью.
Очевидно, все это знали. Не говоря уже обо всех теориях, которые не были напрямую связаны со стандартными гипотезами Гротендика. Не будет преувеличением сказать, что эти гипотезы определяли будущее области алгебраической геометрии. Он взял ручку и начал писать на доске.
[… Когда i≤n/2, квадратичная форма X на A^i(X)∩ker(L^(n−2i+1))→(−1)^i·L^(r−2i) x.x является положительно определённой…
[X — это гладкая проекция алгебраического кластера в области k, где l — простое число, взаимно простое с характеристикой k, H^i(X, Ql) — это i-адическая группа когомологий X. Гиперплоскость проекционного пространства X пересекает подсемейство алгебраических многообразий X. 𝘙ÄΝőᛒÊṡ
[Когда X является алгебраической поверхностью или сложным алгебраическим кластером, эта гипотеза верна.]
Однако он хотел доказать, что эта гипотеза верна для всех случаев X!
Время быстро шло.
На доске появлялось всё больше и больше вычислений. Скорость понимания аудитории не могла сравниться со скоростью письма Лу Чжоу. Перельман сидел в толпе, скрестив руки на груди. Внезапно он выпрямился и нахмурился, глядя на доску. Шольце, сидевший рядом, недоверчиво воскликнул:
«Он использовал метод когомологий L^2, чтобы получить топологическую абстракцию компактного фактор-пространства полного многообразия. Это расширяет теорию Ходжа на компактные многообразия до некомпактных! Господи Иисусе!… Он гений!”
Это свойство теории когомологий L^2 было упомянуто в статье о дискретных группах и эллиптических операторах, опубликованной сэром Атья в «The Mathematics Yearbook» в 1976 году. Что удивило Шольце, так это не изобретательность Лу Чжоу, а то, как легко Лу Чжоу применил эти математические инструменты. Казалось, что Лу Чжоу знал эти математические инструменты как свои пять пальцев. Перельман посмотрел на Шольце и сказал: «Да, очевидно».
Неподалёку, в зале. Там сидели два старика и смотрели на доску. Когда Лу Чжоу успешно применил теорию Ходжа на компактных многообразиях к некомпактным многообразиям, профессор Делинь внезапно нарушил тишину.
— Что ты думаешь?
Фальтингс сидел рядом с ним и молчал. Через 10 секунд он покачал головой.
— Мне нужно время, чтобы подумать об этом… Может быть, я слишком стар.
Делинь с достоинством посмотрел на сцену.
Читайте ранобэ Передовая Технологическая Система Учёного на Ranobelib.ru
Он впервые услышал, как старик Фальтингс говорит о своём возрасте. Услышав, как старик сам в этом признаётся, он немного расстроился… С другой стороны, в зале происходил ещё один разговор. Цю Чэнтун задал профессору Тао вопрос. Будучи экспертом в широком спектре областей математики, он, вероятно, был одним из немногих, кто мог угнаться за Лу Чжоу.
Ему пришлось выложиться по полной. Даже ему было трудно угнаться за Лу Чжоу.
«Его скорость мышления слишком высока… Это похоже на то, как обычные люди думают со скоростью автомобиля, я думаю со скоростью ракеты Space-X, но он думает со скоростью света. Прежде чем я успеваю уловить ход его мыслей, он уже решает задачу».
Поскольку жена Тао Теренса работала в НАСА, он часто проводил аэрокосмические аналогии.
Старик Цю не обращал внимания на Тао Теренса и продолжал смотреть на доску. Через некоторое время он сжал кулак и пробормотал: «Потрясающе».
…
Не было никаких сомнений в том, что это был самый славный момент в истории китайской математики. Нет, не только китайской математики. Это был самый значимый момент в истории математики, и точка. Он не только стоял на вершине математической пирамиды, но и олицетворял собой вершину человеческого разума. Перед доской, которая соединяла человеческий разум со Вселенной, такие вещи, как национальность, раса и культурное происхождение, меркли по сравнению с этим. Такие тривиальные детали, как эти, стали бессмысленными.
Лу Чжоу записал последний символ.
В зале стояла гробовая тишина.
На самом деле, несколько минут назад лишь горстка людей знала, что это произойдёт.
Лу Чжоу сделал два шага назад и посмотрел на свои записи почти как на произведение искусства. Прошло несколько минут, прежде чем он повернулся и обратился к молчаливой аудитории.
«Это моё доказательство стандартных гипотез Гротендика. Quod erat demonstrandum*».
(*латынь — Что и требовалось доказать)
На всём стадионе воцарилась тишина. Не было слышно ни звука. Никто не говорил. Никто не хлопал в ладоши. Торжественные и эмоциональные выражения лиц сменились усталостью и шоком. Лу Чжоу посмотрел на собравшихся.
«Теория Великого объединения — тема этого доклада. Доказательство стандартных гипотез Гротендика — лишь пример. Я надеюсь, что это вдохновит на дальнейшие исследования. То, что мы стали свидетелями, — это доказательство того, что Вселенная идеально соответствует математической красоте. Есть вопросы?»
Толпа молчала. Никто не говорил. Лу Чжоу расслабил плечи. Казалось, что с его плеч только что свалилась тысяча килограммов. На его лице внезапно появилась приятная улыбка. В этой улыбке не было ничего необычного, но она находила отклик в сердце каждого слушателя.
— Если вопросов нет, я завершу доклад. Я буду здесь в течение следующих трёх дней, так что, если у кого-нибудь возникнут вопросы, вы можете найти меня. Спасибо.
Аплодисменты прозвучали как раскаты грома.
Они полностью заполнили спортзал. Лу Чжоу видел шок и удивление в глазах людей. Казалось, что кто-то включил звук в мире.
Сотрудники, стоявшие по краям зала, а также охранники выглядели растерянными. Они явно не понимали, что происходит. Не все понимали красоту математики. Однако для тех, кто это сделал, красота потрясла и отозвалась в глубине их душ. Аплодисменты были подобны песне. Под оглушительные аплодисменты Лу Чжоу положил свой маркер на подиум, сделал шаг назад и слегка поклонился. Затем он развернулся и ушёл со сцены. Эпоха стандартных гипотез Гротендика закончилась. С этого момента мир вступил в новую эру математики!