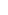Под наплывом вдохновения Лу Чжоу, не останавливаясь, писал. Он даже забыл про еду.
Парня переполняла мотивация, и он был безгранично воодушевлен.
«Существует группа G и |G / =р1 а1 р2а2 piai, где pi — простое число, a ai — положительное целое число. Пусть pGn (G), определим deg (p)=|{qGn (G)|p~q).
Число раз, когда deg (p) является вершиной р. обозначим как C (G)=…»
Время шло, но Лу Чжоу писал, не останавливаясь.
Это не так, как в прошлый раз…
В прошлый раз вдохновение было вынужденное, но сейчас оно — его.
Ручка скользила по бумаге.
Сам того не сознавая, Лу Чжоу уже исписал пять страниц.
Закончив с шагами и основными идеями, парень потер живот и облокотился на спинку, потом достал телефон.
Лу Чжоу удивился, увидев время.
— Черт, уже пять часов?!
Парень даже не позавтракал.
Уже не в состоянии терпеть, Лу Чжоу пошел в забитую столовую и поужинал, после чего вернулся к работе.
В шесть вечера Ши Шан вернулся с едой в руках, увидев, что Лу Чжоу пишет, он любопытно спросил:
— Что делаешь, Чжоу? У магистров тоже есть домашка?
Парень был в ключевом месте, поэтому ответил, не поднимая головы:
— Пишу статью.
В это время внезапно Хуан Гуанмин и Лю Жуй тоже вернулись с едой.
Лю Жуй бросил рюкзак на стол и достал свою домашнюю работу, а Хуан Гуанмин подошел к Лу Чжоу и с любопытством посмотрел, что тот пишет.
Но Хуан Гуанмин ничего не понял.
— Черт, Чжоу, я ничерта не понимаю из того, что ты написал.
Из любопытства… Ши Шан тоже подошел.
— Гуанмин, мы уже — на третьем курсе, так что ты должен хотя бы понимать символы… Нихрена себе, это — теория групп… сложная вещь!
Лю Жуй, начавший делать домашнее задание, повертел ручкой и произнес:
— Это не настолько сложно, многие на четвертом курсе проходят это. Но это никак не связано с нашей специальностью… Ну, если только вы не переводитесь на теоретическую физику…
Прикладная математика и теоретическая физика — похожи, так что нет ничего необычного в переводе.
Многие переводятся из-за большого финансирования теоретической физики.
— Я не смогу перевестись, — произнес Хуан Гуанмин, покачав головой и медленно отходя.
— Конечно, ты не можешь, ты — не такой, как Лу Чжоу, — сказал Ши Шан и похлопал Гуанмина по плечу с печальным видом.
Лу Чжоу не понимал, что происходит.
Рим построили не за один день. Хорошая теория требует не только вдохновения, но и времени.
Читайте ранобэ Передовая Технологическая Система Учёного на Ranobelib.ru
В течение следующих нескольких дней парень проводил все свое время в библиотеке и в общежитии.
Время от времени Лу Чжоу отвечал на почту от профессора Фрэнка Вильчека. Однако, поскольку новых данных из ЦЕРНа не поступало, ему особо не пришлось ничего делать дополнительно.
Лу Чжоу был удовлетворен каждым прожитым днем.
Хотя для других это непостижимо, но Лу Чжоу был счастлив.
На второй неделе сентября, солнечным утром, Лу Чжоу, сидевший в библиотеке, взглянул на десятки бумаг, лежащих перед ним, и с облегчением произнес:
— Наконец-то!
Парень решил проблему, когда пришло вдохновение. И теперь он уже видел выход из этого лабиринта перед глазами.
Лу Чжоу был уставший, но одновременно с этим испытывал удовлетворение.
И не только оттого, что он решил еще одну математическую проблему, но и потому что он глубже понял теорию групп, что позволило ему разработать новый математический метод.
Это интереснее самого доказательства.
Гильберт однажды сказал, что великая теорема Ферма — курица, несущая золотые яйца, и не потому что накормила множество математиков или дала многим журналам возможность опубликовать множество «воды» по этой теме, а потому, что благодаря ней появились многие новые математические методы.
Вдохновленный проблемой Ферма, Куммер ввел понятие идеальных чисел и нашел единственную теорему о разложении, которая разбивает числа круговой области на идеальный простой фактор. К сегодняшнему дню эту теорему развили Дедекинд и Кронекер. Она заняла центральное место в теории современных чисел, и ее значение выходило далеко за рамки теории чисел и вошло даже в функциональную алгебру.
Работа Лу Чжоу на Принстонской конференции — такая же. Его метод топологии решил гипотезы чисел-близнецов.
Первоначально теорию решета применил Чэнь Цзинжунь, и сообщество теории чисел полагало, что для решения гипотезы Гольдбаха в форме «один плюс дин» им понадобиться новый метод.
Теперь оказалось, что этот метод — более полезный, чем они думали.
Даже профессор, который выдвинул теорию решета в тысяча девятьсот девяносто пятом году, не ожидал этого.
В этом и заключается ценность теории чисел.
Лу Чжоу не только доказал гипотезу Полиньяка, но и нашел уникальное решение.
Парень назвал этот метод «методом исследования структуры теории групп» или «методом групповой структуры» для краткости.
Используя метод теории групп, проблема бесконечности изучалась в целом. Форма «К=1» расширялась до «к — бесконечное натуральное число», что доказывает, что «для всех натуральных чисел к существует бесконечно много пар простых чисел (р, р+2к)».
Вывод — лишь в одном предложении, но для доказательства потребуется несколько досок.
Парень потратил весь день, чтобы собрать воедино доказательство и оформить его.
Глядя на готовую статью, Лу Чжоу с удовлетворением кивнул.
— Пожалуй, достаточно.
Он мог более детально написать о своем методе.
Но этот метод — не основа его статьи.
В первую очередь гипотеза Полиньяка — доказана.
Хотя с виду это лишь продолжение его доказательства о числах-близнецах, но истинная сложность известна лишь ему.
Лу Чжоу подумал и добавил строку в конце статьи.
«Из-за объема, теория групповой структуры будет подробно объяснена в следующей статье.»
Загрузить!
Цель, «Математический ежегодник»!